No.154 市バス｜yukicoder

No.154 市バス - yukicoderを解きました。

この問題、文字列の問題を探していて星★★だったし解けるかな〜？みたいな
軽い気持ちで適当に選んだのが全ての始まりでした...(序章)

初めはstd::findで文字列を見つけて場合分けすればいけるのでは(？)
みたいな感じでコードを書いて提出....WA...WA...WA...。

std::findではダメだったので、普通に1文字ずつ見て場合分けを考えました。
その際、可否判定をした文字列自体をtempに持つ解法で考えていました...。

この辺りで周辺から｢この問題は文字列の問題だけど文字列の問題ではない｣みたいな事を言われ出す...
そして文字をカウントして比較していく解法という事を知り得る。
この部分が自分で気付けなかったのでこの問題は実質自分では解けなかった事になった。

// 考え方

※reverseして後ろから見ていく解法です

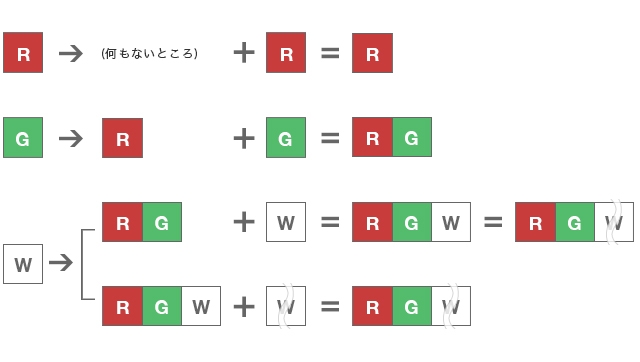
Rが来た場合
・バスの系統が発生する

Gが来た場合
・Gに対応するRがある場合､｢R｣に｢G｣を連結させて｢RG｣となる
・Gに対応するRがない場合、正しい系統不成立となりimpossible.

Wが来た場合
・Wに対応するRGがある場合､｢RG｣に｢W｣を連結させて｢RGW｣となる
・Wに対応するRGがなく､RGW+がある場合は｢RGW+｣に｢W｣を連結させて｢RGW+｣となる
　(※+は1つ以上のWを指す)
・Wに対応する｢RG｣,｢RGW+｣のいづれもない場合は正しい系統不成立となりimpossible.

以上の考察を踏まえて提出したコード↓

#include <bits/stdc++.h>
#define REP(i,n) for(int i=0; i<(n); i++)
using namespace std;
/*関数化ver*/
bool check( string S ){
    int R{}, G{}, W{};
    REP( i, (int)S.size() ){
        //Rが来たら系統を増やす
        if( S[i] == 'R' ){
            R++;
        }
        //Rを持っているGが来たらG++,R--する
        if( S[i] == 'G' ){
            if( R >= 1 ){
                G++;
                R--;
            }else{
                //Rを持たないGはfalse
                return false;
            }
        }
        //Wの場合は3つの選択肢がある
        if( S[i] == 'W' ){
            //RGを持つ場合
            if( G >= 1 ){
                G--;
                W++;
            //RGが無く,RGW+を持っている場合
            }else if( W >= 1 ){
                W++;
            //RG,RGW+のいづれも持たない場合
            }else{
                return false;
            }
        }
    }
    if( R == 0 && G == 0 ){
        return true;
    }
    return false;
}
int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);
    
    int N;
    cin >> N;
    
    string S;
    while( cin >> S ){
        reverse( S.begin(), S.end() );
        cout << ( check( S ) ? "possible" : "impossible" ) << endl;
    }
    return 0;
}

実装自体は難しい事は無く、場合分けで書けるのですが、考察がきちんと出来ていないと
全ての条件を網羅出来ないので険しい感じでした。
(私が最後まで理解出来なかったのはRGが無く､RGW+を持っている場合でした...)

今まで深く考察して解くような問題を解いた事がなかったので、
かなり時間が掛かってしまったのですが、最後まで実装出来て良かったです。

それと色々な方の提出が見れたのも大変勉強になりました！
提出一覧 - yukicoder

まだ解いた事ない方は学習的な良問なので是非！！
No.154 市バス - yukicoder