2019年 進捗大反省会

年末なので今年 1 年の振り返り記事を書きます。

仕事

• 転職して 1 年くらい経ちましたが何とか順調です。緊急度や、重要度の高い Project にアサインされる事も増えて、今年は夏休みも消えた...（年末年始休みは無事確保）
• 各部署の人との繋がりもできてきて、仕事がしやすくなった（感謝）
• 遅刻もあまりしなくなった
• スタバにほぼ毎日行ってたくさん課金した

競プロ

• 今年はABC埋めを暇を見つけてやりました
• Union-Find をちょっと勉強した
• 算数もちょっと勉強した
• 何していいか最近良く判らない

読んだ本

• シェルスクリプトの本（リファレンスに近いもの）を読み途中
• 金融の本
• 英語学習の本数冊

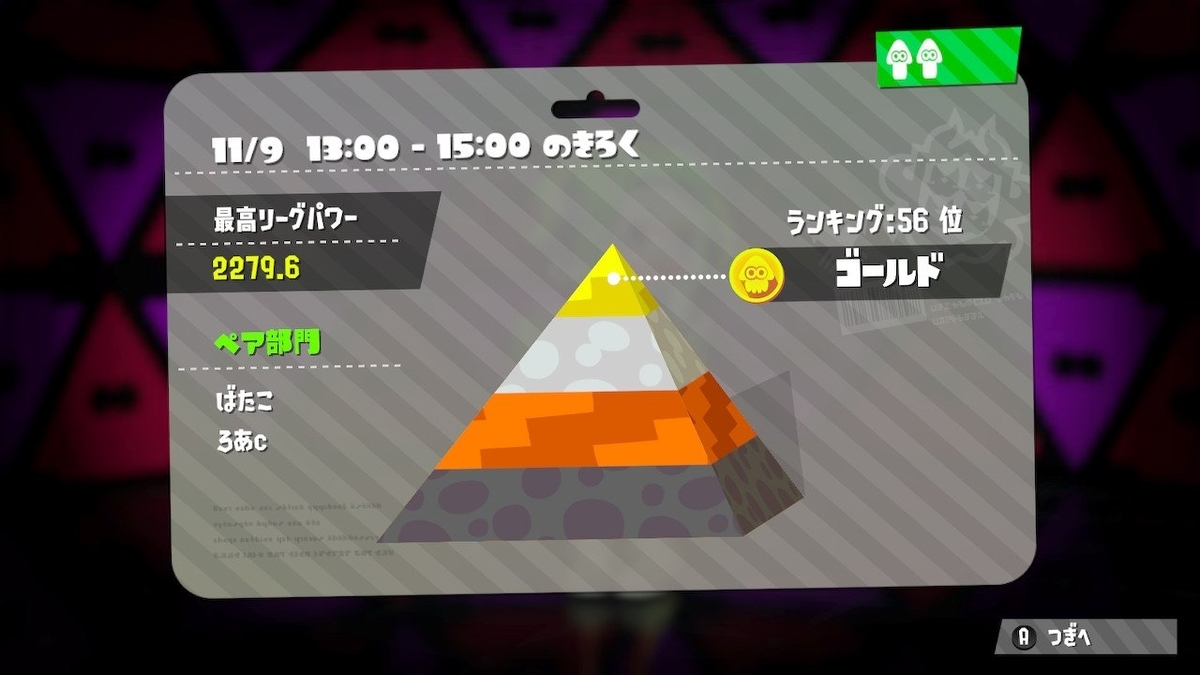
ゲーム

• スプラトゥーン2 でたくさん遊んだ。今年はレッドコーダーに囲まれてリーグマッチする機会もあって緊張した...。去年から引き続き競プロ勢とわいわい遊んでもらった。年々遊んでくれる人が増えてうれしい。
• ばたこさんと 2 人リーグマッチで初めてゴールド取れた（画像参照）
• 生まれて初めて、ポケモン（ソード）もやった

その他

• Uber Eats にハマった（オーダーする方、おすすめ）
• Apple Watch 買った（仕事で使う予定だったけど Project 消えた）
• iPad Pro 買った（競プロの考察が捗った、おすすめ）
• APIサーバーを立てようとした（立ててはいない、途中）
• 同僚の結婚式に呼ばれて行った（かわいかった）
• オンライン英会話の体験をしたが 1 回で挫折（コミュ障には敷居高かった）

色々書いたけど、今年はほぼ職場と家との往復で帰って寝るだけ生活が続いた...(疲労)

2020年の目標

• 趣味の時間ほしい
• 江添先生のC++入門を絶対読みたい
• バックエンドの勉強をしたい
• 英語の勉強を引き続きする
• 物を増やさない（目指せミニマリスト）
• ストレスをためないようにしたい
• Twitterもしようかな？

2020年もよろしくお願いします（おわり）

ABC131 A - Security｜std:: adjacent_find｜C++

A - Security を解きました。

std::adjacent_find

std::adjacent_find は隣接する要素で条件を満たしている最初の要素を検索してくれます *1

[first,last) 内にあるイテレータ i について、*i == *(i + 1) となる要素を見つけた場合、
最初のイテレータを返します。
見つからなかった場合は last を返します。

これを利用して、隣接する要素が同じ値かどうかを判定しました。
std::adjacent_find は便利

#include <bits/stdc++.h>
using namespace std;
#define ALL(n) begin(n),end(n)
struct cww{cww(){ios::sync_with_stdio(false);cin.tie(0);}}star;
int main()
{
    string S;
    cin >> S;
    cout << (S.end() == adjacent_find(ALL(S)) ? "Good" : "Bad") << endl;
    return 0;
}

*1:adjacent_find - cpprefjp C++日本語リファレンス

ABC128 B - Guidebook｜tuple

B - Guidebook を解きました。
sort の工夫を覚えたのでメモ

題意

• 個のレストランの 所在市名 と評価 が与えられる
• 以下の順でレストランの番号を出力する
  • 市名が辞書順で早いものから
  • 同じ市に複数レストランがある場合は、評価が高いものから

考察

• 保持しなくてはいけない情報は [ 市名 ][ 評価 ][ レストラン番号 ]の3つ
• 値を 3 つ保持するために std::tuple *1 を使用する
• 辞書順かつ評価の降順で sort するというのが厄介だが、負号()を付けることで コンテナを sort するだけで上手く並ぶので負号を付与して要素構築する

辞書順 sort しただけ
aa 10
ab 30
ab 50

符号を付けて辞書順 sort
aa -10
ab -50
ab -30

#include <bits/stdc++.h>
using namespace std;
#define ALL(n) begin(n),end(n)
struct cww{cww(){ios::sync_with_stdio(false);cin.tie(0);}}star;
int main()
{
    int N;
    cin >> N;
    vector<tuple<string, int, int>> v;
    for (int i = 0; i < N; ++i)
    {
        string S;
        int P;
        cin >> S >> P;
        v.emplace_back(S, -P, i + 1); // P_i に負号付与
    }
    sort(ALL(v));
    for (auto &x : v)
    {
        cout << get<2>(x) << endl;
    }
    return 0;
}

こんな単純なことで条件を満たすとは...。
計算量は全体で .

*1:std::tuple の使い方｜C++ - C++競プロ学習日記(仮)

VSCode の Snippet に競プロ用テンプレを設定する方法

VSCodeで新規ファイルを開いた時に tmp と打つと自分のテンプレが追加されるようにしたのでメモ

設定環境：MacOS 10.14.3 ／ VSCode 1.32.1

Code ➡ Preferences ➡ User Snippets と進む

gitで管理している競プロ用フォルダ c-pro の中に作りたいので、
New Snippets file for 'c-pro' ... を選択します。

{
    "Print to console": {
        "prefix": "tmp",
        "body": [
            "#include <bits/stdc++.h>",
            "using namespace std;",
            "#define REP(i,n) for(int i=0; i<(n); i++)",
            "#define REP2(i,x,n) for(int i=x; i<(n); i++)",
            "#define ALL(n) begin(n),end(n)",
            "struct cww{cww(){ios::sync_with_stdio(false);cin.tie(0);}}star;",
            "const long long INF = numeric_limits<long long>::max();",
            "int main()",
            "{",
            "    return 0;",
            "}"
            ],
        "description": "template"
    }
}

選択すると、名称未設定.code-snippets というファイルが出来るのでそこに展開したいテンプレートを json で書きます。

"prefix": で設定した text を打つとサジェストされるようになります。
"body": は展開される中身(テンプレ)
"description": は Snippet 使い分けるために書いておいた方が良さそう

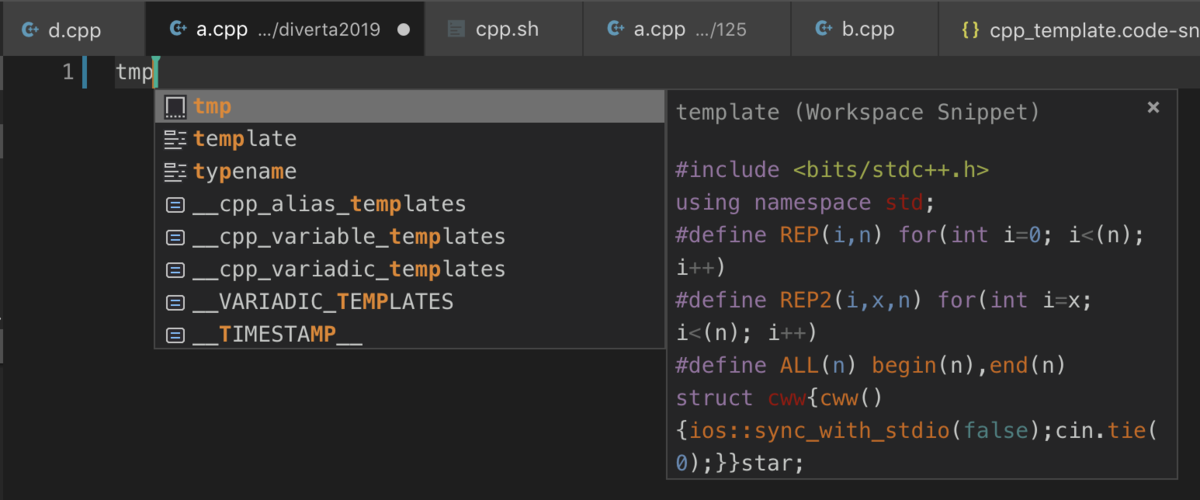
tmp って打つとサジェストされる

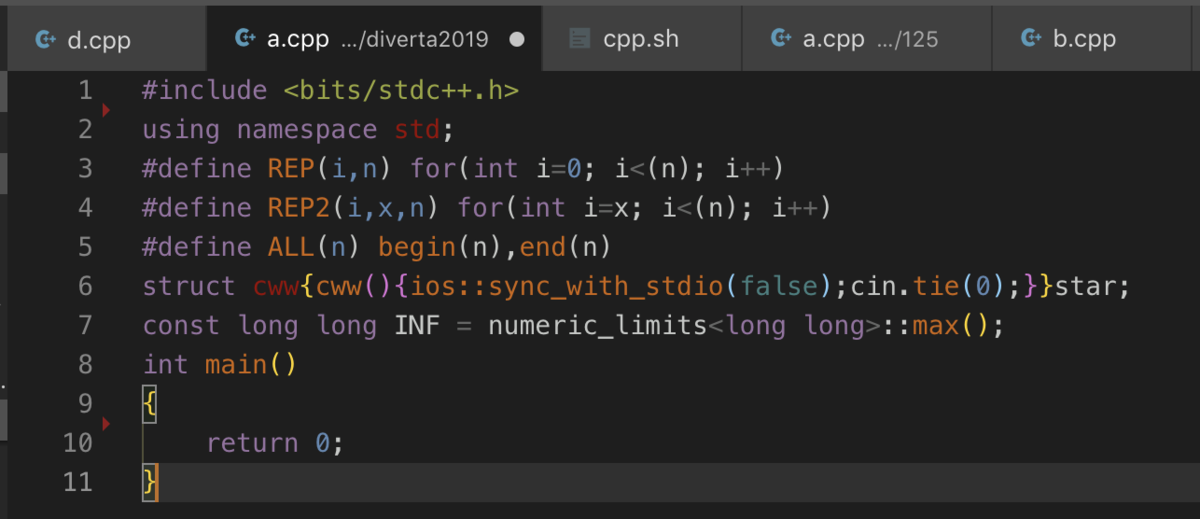
無事テンプレ展開されるようになりました！
簡単便利！

約数列挙｜C++

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int N;
    cin >> N;
    
    vector<int> v;
    for( int i = 1; i <= N; i++ )
    {
        if( N % i == 0 )
        {
	       v.emplace_back( i );
        }
    }
    for( auto &x : v )
    {
        cout << x << " ";
    }
    cout << endl;
    cout << "count : " << v.size() << endl;
    return 0;
}

INPUT

100

OUTPUT

1 2 4 5 10 20 25 50 100 
count : 9

実行コード：[Wandbox]三へ( へ՞ਊ ՞)へ ﾊｯﾊｯ