No.7 プライムナンバーゲーム|yukicoder|メモ化再帰
No.7 プライムナンバーゲーム - yukicoder を 1ヶ月半 かけて解きました。
(何故 1ヶ月かかったのかは後述)
題意:
・はじめに先攻プレイヤーに自然数 N が与えられます。
・N以下の素数のどれかで減算し相手に渡す、を先攻・後攻で交互に繰り返し、
N が 0 か 1 になったら負けとなる。
・自分(先攻)が勝つ場合は"Win", 負ける場合は"Lose"を出力します。
・ゲームは互いに最善を尽くすものとする。
・2 ≤ N ≤ 10000
考察①:グラフを描く
まず、N = 7 の場合のプライムナンバーゲームの状態をグラフに描いて考えました。
先攻プレーヤーの持ち点 7 を根とし、子ノードの値となるのは N - ( N 以下の素数 ) です。
N == 0 か N == 1 を作った方が負けという観点から、 0 か 1 を受け取った方が勝ちと考えます。
ピンクの頂点が、先手勝ちとなる選択が存在する局面です。

この様に、ゲームの状態を頂点にして、遷移可能な状態を辺で結んだグラフを一般に ゲーム木 *1と呼びます。
ゲーム木上の子ノードの局面において、全ての値に対する勝敗のAND/ORを取ると、
・先手番時に先手勝ちが一つでもあれば先手勝ち(OR)
・後手番時に全て先手勝ちなら先手の勝ち(AND)
となる事が判ります。
この様に、2人で対戦し勝敗のみを気にするゲームのゲーム木をAND/OR木 *2 と呼びます。
以上を踏まえ、例に挙げた N = 7 の場合の勝敗( Win/Lose )を考えると、
下記図の様に 先手勝ち( Win ) となる事が判ります。
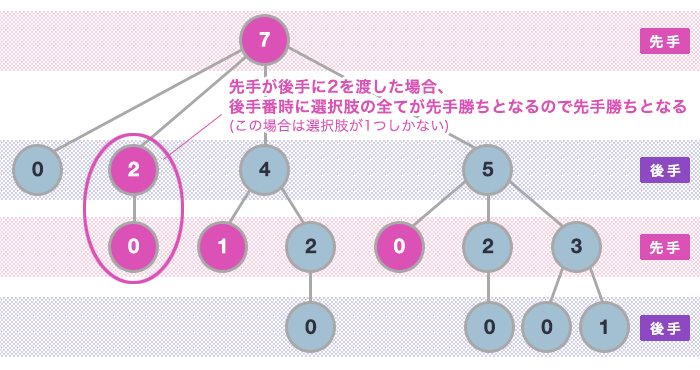
ここまで判ったら、ゲームに関する考察は終わりで、これをそのまま実装する事となります。*3
考察②:素数の準備
与えられた N から N以下の素数 で引く為、N 以下の素数列挙が必要となります。
O( N^2 ) での列挙では TLE する為、O(N^2)より早くする必要があります。
素数列挙方法につきましては長くなる為、以下別記事に O( N√N ) ver と O( N log log N ) ver の2つを書きました。
考察③:計算量を減らす
考察②までを終えて提出した結果、N = 9299 のケースでTLE してしまいました。
何が無駄かを考える為に、ここでもう一度 グラフ を見ます。
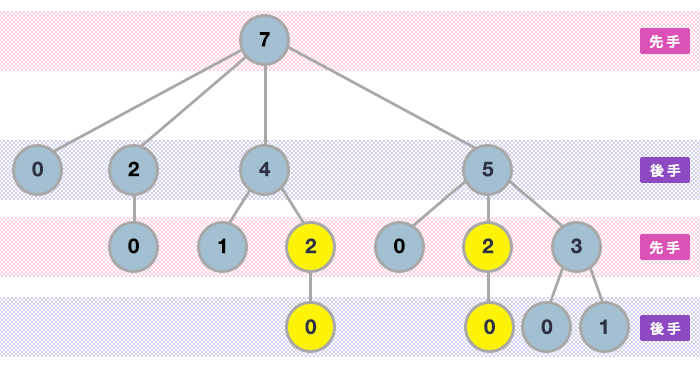
先手番時に同じ値を持つ部分木(黄色い頂点) が2回出現している事がグラフを見ると判ります。
この図は N = 7 の場合なので同じ値を持つ部分木の数が少ないですが、
N = 10000 の場合を考えると、もっと膨大な同じ値を持つ部分木が出現するのが予想できます。
そこで、一度訪れた頂点の勝敗結果を記憶し、既に訪問済みであれば記憶した結果を返すようにする事で計算量を減らします。
それを一般に メモ化 と呼ぶようです。*4
実装:
#include <bits/stdc++.h> using namespace std; struct cww{cww(){ios::sync_with_stdio(false);cin.tie(0);}}star; int N; vector<int> P; vector<vector<int>> visit( 2, vector<int>( 10001, -1 ) );//<---初期化!!! void prime( int N ) { for( int i = 2; i <= N; i++ ) { bool flag = true; for( int j = 2; j * j <= i; j++ ) { if( i % j == 0 ) { flag = false; break; } } if( flag ) { P.emplace_back( i ); } } reverse( P.begin(), P.end() ); } bool dfs( const int T, const int N ) { if( N == 0 || N == 1 ) { return T == 0 ? 1 : 0; } if( visit[ T ][ N ] >= 0 ) { return visit[ T ][ N ]; } if ( T == 0 ) { for( const auto &x : P ) { if( N - x >= 0 ) { if( dfs( 1, N - x ) ) { visit[ T ][ N ] = 1; return 1; } } } visit[ T ][ N ] = 0; return 0; } else { for( const auto &x : P ) { if( N - x >= 0 ) { if( !dfs( 0, N - x ) ) { visit[ T ][ N ] = 0; return 0; } } } visit[ T ][ N ] = 1; return 1; } } int main() { cin >> N; prime( N ); cout << ( dfs( 0, N ) ? "Win" : "Lose" ) << endl; return 0; }
まとめ:
考察 4 : 実装 6 くらいの割合で 1か月半 を消費した気がします。
考察では、グラフの基礎やゲーム木・AND/OR木の概念を学習、ゲームの状態を考察するのにグラフも沢山描きました。
実装では、素数列挙のアルゴリズム・エラトステネスの篩(ふるい)を学習したり、計算量を落とすメモ化も初めて書きました。
他にも実装面ではかなり細かい部分で消費しました。
(二次元配列の正しい要素数確保(今更)、メモリの概念(今更) とか...)
色んな学習要素が含まれている問題で、予想外に時間が掛かりましたが、
年内に AC 出来て良かったです(年内怪しいかな...って思ってた)。
※この記事を書いたのは昨年末です(公開するの忘れていた)